Review Exercises
Find Equivalent Fractions
In the following exercises, find three fractions equivalent to the given fraction. Show your work, using figures or algebra.
| 1. \(\dfrac{1}{4}\) | 2. \(\dfrac{1}{3}\) |
| 3. \(\dfrac{5}{6}\) | 4. \(\dfrac{2}{7}\) |
Simplify Fractions
In the following exercises, simplify.
| 5. \(\dfrac{7}{21}\) | 6. \(\dfrac{8}{24}\) |
| 7. \(\dfrac{15}{20}\) | 8. \(\dfrac{12}{18}\) |
| 9. \(-\dfrac{168}{192}\) | 10. \(-\dfrac{140}{224}\) |
| 11. \(\dfrac{11x}{11y}\) | 12. \(\dfrac{15a}{15b}\) |
Multiply Fractions
In the following exercises, multiply.
| 13. \(\dfrac{2}{5}\cdot \dfrac{1}{3}\) | 14. \(\dfrac{1}{2}\cdot \dfrac{3}{8}\) |
| 15. \(\dfrac{7}{12}(-\dfrac{8}{21})\) | 16. \(\dfrac{5}{12}(-\dfrac{8}{15})\) |
| 17. \(-28p(-\dfrac{1}{4})\) | 18. \(-51q(-\dfrac{1}{3})\) |
| 19. \(\dfrac{14}{5}(-15)\) | 20. \(-1(-\dfrac{3}{8})\) |
Divide Fractions
In the following exercises, divide.
| 21. \(\dfrac{1}{2}\)÷\(\dfrac{1}{4}\) | 22. \(\dfrac{1}{2}\)÷\(\dfrac{1}{8}\) |
| 23. \(-\dfrac{4}{5}\)÷\(\dfrac{4}{7}\) | 24. \(-\dfrac{3}{4}\)÷\(\dfrac{3}{5}\) |
| 25. \(\dfrac{5}{8}\)÷\(\dfrac{a}{10}\) | 26. \(\dfrac{5}{6}\)÷\(\dfrac{c}{15}\) |
| 27. \(\dfrac{7p}{12}\)÷\(\dfrac{21p}{8}\) | 28. \(\dfrac{5q}{12}\)÷\(\dfrac{15q}{8}\) |
| 29. \(\dfrac{2}{5}\)÷\(\left(-10\right)\) | 30. \(-18\)÷\(-\left(\dfrac{9}{2}\right)\) |
| 31. \(\dfrac{\dfrac{2}{3}}{\dfrac{8}{9}}\) | 32. \(\dfrac{\dfrac{4}{5}}{\dfrac{8}{15}}\) |
| 33. \(\dfrac{-\dfrac{9}{10}}{3}\) | 34. \(\dfrac{2}{\dfrac{5}{8}}\) |
| 35. \(\dfrac{\dfrac{r}{5}}{\dfrac{s}{3}}\) | 36. \(\dfrac{-\dfrac{x}{6}}{-\dfrac{8}{9}}\) |
Simplify Expressions Written with a Fraction Bar
In the following exercises, simplify.
| 37. \(\dfrac{4+11}{8}\) | 38. \(\dfrac{9+3}{7}\) |
| 39. \(\dfrac{30}{7-12}\) | 40. \(\dfrac{15}{4-9}\) |
| 41. \(\dfrac{22-14}{19-13}\) | 42. \(\dfrac{15+9}{18+12}\) |
| 43. \(\dfrac{5\cdot 8}{-10}\) | 44. \(\dfrac{3\cdot 4}{-24}\) |
| 45. \(\dfrac{15\cdot 5-{5}^{2}}{2\cdot 10}\) | 46. \(\dfrac{12 \cdot 9-{3}^{2}}{3\cdot 18}\) |
| 47. \(\dfrac{2+4\left(3\right)}{-3-{2}^{2}}\) | 48. \(\dfrac{7+3\left(5\right)}{-2-{3}^{2}}\) |
Translate Phrases to Expressions with Fractions
In the following exercises, translate each English phrase into an algebraic expression.
| 49. the quotient of c and the sum of d and 9. | 50. the quotient of the difference of h and k, and \(-5\). |
Add and Subtract Fractions with a Common Denominator
In the following exercises, add.
| 51. \(\dfrac{4}{9}+\dfrac{1}{9}\) | 52. \(\dfrac{2}{9}+\dfrac{5}{9}\) |
| 53. \(\dfrac{y}{3}+\dfrac{2}{3}\) | 54. \(\dfrac{7}{p}+\dfrac{9}{p}\) |
| 55. \(-\dfrac{1}{8}+\left(-\dfrac{3}{8}\right)\) | 56. \(-\dfrac{1}{8}+\left(-\dfrac{5}{8}\right)\) |
In the following exercises, subtract.
| 57. \(\dfrac{4}{5}-\dfrac{1}{5}\) | 58. \(\dfrac{4}{5}-\dfrac{3}{5}\) |
| 59. \(\dfrac{y}{17}-\dfrac{9}{17}\) | 60. \(\dfrac{x}{19}-\dfrac{8}{19}\) |
| 61. \(-\dfrac{8}{d}-\dfrac{3}{d}\) | 62. \(-\dfrac{7}{c}-\dfrac{7}{c}\) |
Add or Subtract Fractions with Different Denominators
In the following exercises, add or subtract.
| 63. \(\dfrac{1}{3}+\dfrac{1}{5}\) | 64. \(\dfrac{1}{4}+\dfrac{1}{5}\) |
| 65. \(\dfrac{1}{5}-\left(-\dfrac{1}{10}\right)\) | 66. \(\dfrac{1}{2}-\left(-\dfrac{1}{6}\right)\) |
| 67. \(\dfrac{2}{3}+\dfrac{3}{4}\) | 68. \(\dfrac{3}{4}+\dfrac{2}{5}\) |
| 69. \(\dfrac{11}{12}-\dfrac{3}{8}\) | 70. \(\dfrac{5}{8}-\dfrac{7}{12}\) |
| 71. \(-\dfrac{9}{16}-\left(-\dfrac{4}{5}\right)\) | 72. \(-\dfrac{7}{20}-\left(-\dfrac{5}{8}\right)\) |
| 73. \(1+\dfrac{5}{6}\) | 74. \(1-\dfrac{5}{9}\) |
Use the Order of Operations to Simplify Complex Fractions
In the following exercises, simplify.
| 75. \(\dfrac{{\left(\dfrac{1}{5}\right)}^{2}}{2+{3}^{2}}\) | 76. \(\dfrac{{\left(\dfrac{1}{3}\right)}^{2}}{5+{2}^{2}}\) |
| 77. \(\dfrac{\dfrac{2}{3}+\dfrac{1}{2}}{\dfrac{3}{4}-\dfrac{2}{3}}\) | 78. \(\dfrac{\dfrac{3}{4}+\dfrac{1}{2}}{\dfrac{5}{6}-\dfrac{2}{3}}\) |
Evaluate Variable Expressions with Fractions
In the following exercises, evaluate.
| 79. \(x+\dfrac{1}{2}\) when a) \(x=-\dfrac{1}{8}\) b) \(x=-\dfrac{1}{2}\) |
80. \(x+\dfrac{2}{3}\) when a) \(x=-\dfrac{1}{6}\) b) \(x=-\dfrac{5}{3}\) |
| 81. \(4{p}^{2}q\) when \(p=-\dfrac{1}{2}\) and \(q=\dfrac{5}{9}\) | 82. \(5{m}^{2}n\) when \(m=-\dfrac{2}{5}\) and \(n=\dfrac{1}{3}\) |
| 83. \(\dfrac{u+v}{w}\) when \(u=-4,v=-8,w=2\) |
84. \(\dfrac{m+n}{p}\) when \(m=-6,n=-2,p=4\) |
Name and Write Decimals
In the following exercises, write as a decimal.
| 85. Eight and three hundredths | 86. Nine and seven hundredths |
| 87. One thousandth | 88. Nine thousandths |
In the following exercises, name each decimal.
| 89. 7.8 | 90. 5.01 |
| 91. 0.005 | 92. 0.381 |
Round Decimals
In the following exercises, round each number to the nearest a) hundredth b) tenth c) whole number.
| 93. 5.7932 | 94. 3.6284 |
| 95. 12.4768 | 96. 25.8449 |
Add and Subtract Decimals
In the following exercises, add or subtract.
| 97. \(18.37+9.36\) | 98. \(256.37-85.49\) |
| 99. \(15.35-20.88\) | 100. \(37.5+12.23\) |
| 101. \(-4.2+\left(-9.3\right)\) | 102. \(-8.6+\left(-8.6\right)\) |
| 103. \(100-64.2\) | 104. \(100-65.83\) |
| 105. \(2.51+40\) | 106. \(9.38+60\) |
Multiply and Divide Decimals
In the following exercises, multiply.
| 107. \(\left(0.3\right)\left(0.4\right)\) | 108. \(\left(0.6\right)\left(0.7\right)\) |
| 109. \(\left(8.52\right)\left(3.14\right)\) | 110. \(\left(5.32\right)\left(4.86\right)\) |
| 111. \(\left(0.09\right)\left(24.78\right)\) | 112. \(\left(0.04\right)\left(36.89\right)\) |
In the following exercises, divide.
| 113. 0.15 ÷ 5 | 114. 0.27 ÷ 3 |
| 115. \$8.49 ÷ 12 | 116. \$16.99 ÷ 9 |
| 117. 12 ÷ 0.08 | 118. 5 ÷ 0.04 |
Convert Decimals and Fractions
In the following exercises, write each decimal as a fraction.
| 119. 0.08 | 120. 0.17 |
| 121. 0.425 | 122. 0.184 |
| 123. 1.75 | 124. 0.035 |
In the following exercises, convert each fraction to a decimal.
| 125. \(\dfrac{2}{5}\) | 126. \(\dfrac{4}{5}\) |
| 127. \(-\dfrac{3}{8}\) | 128. \(-\dfrac{5}{8}\) |
| 129. \(\dfrac{5}{9}\) | 130. \(\dfrac{2}{9}\) |
| 131. \(\dfrac{1}{2}+6.5\) | 132. \(\dfrac{1}{4}+10.75\) |
Identify Integers, Rational Numbers, Irrational Numbers, and Real Numbers
In the following exercises, write as the ratio of two integers.
| 133. a) 9 b) 8.47 | 134. a) \(-15\)b) 3.591 |
In the following exercises, list the a) rational numbers, b) irrational numbers.
| 135. \(0.84,0.79132\text{…},1.\stackrel{\text{-}}{3}\) | 136. \(2.3\stackrel{\text{-}}{8},0.572,4.93814\text{…}\) |
In the following exercises, list the a) whole numbers, b) integers, c) rational numbers, d) irrational numbers, e) real numbers for each set of numbers.
| 137. \(-4,0,\dfrac{5}{6} ,17 ,5.2537\text{…}\) | 138. \(-2, 0.\stackrel{\text{-}}{36},\dfrac{13}{3},6.9152\text{…},10\dfrac{1}{2}\) |
Locate Fractions on the Number Line
In the following exercises, locate the numbers on a number line.
| 139. \(\dfrac{2}{3},\dfrac{5}{4},\dfrac{12}{5}\) | 140. \(\dfrac{1}{3},\dfrac{7}{4},\dfrac{13}{5}\) |
| 141. \(2\dfrac{1}{3},-2\dfrac{1}{3}\) | 142. \(1\dfrac{3}{5},-1\dfrac{3}{5}\) |
In the following exercises, order each of the following pairs of numbers, using < or >.
| 143. \(-1\) ___ \(-\dfrac{1}{8}\) | 144. \(-3\dfrac{1}{4}\)___ \(-4\) |
| 145. \(-\dfrac{7}{9}\) ___ \(-\dfrac{4}{9}\) | 146. \(-2\) ___ \(-\dfrac{19}{8}\) |
Locate Decimals on the Number Line
In the following exercises, locate on the number line.
| 147. 0.3 | 148. -0.2 |
| 149. -2.5 | 150. 2.7 |
In the following exercises, order each of the following pairs of numbers, using < or >.
| 151. 0.9 ___ 0.6 | 152. 0.7 ___ 0.8 |
| 153. -0.6 ___ -0.59 | 154. -0.27 ___ -0.3 |
Use the Commutative and Associative Properties
In the following exercises, use the Associative Property to simplify.
| 155. \(-12\left(4m\right)\) | 156. \(30\left(\dfrac{5}{6}q\right)\) |
| 157. \(\left(a+16\right)+31\) | 158. \(\left(c+0.2\right)+0.7\) |
In the following exercises, simplify.
| 159. \(6y+37+\left(-6y\right)\) | 160. \(\dfrac{1}{4}+\dfrac{11}{15}+\left(-\dfrac{1}{4}\right)\) |
| 161. \(\dfrac{14}{11}\cdot \dfrac{35}{9}\cdot \dfrac{14}{11}\) | 162. \(-18\cdot 15 \cdot \dfrac{2}{9}\) |
| 163. \(\left(\dfrac{7}{12}+\dfrac{4}{5}\right)+\dfrac{1}{5}\) | 164. \(\left(3.98d+0.75d\right)+1.25d\) |
| 165. \(11x+8y+16x+15y\) | 166. \(52m+\left(-20n\right)+\left(-18m\right)+\left(-5n\right)\) |
Use the Identity and Inverse Properties of Addition and Multiplication
In the following exercises, find the additive inverse of each number.
|
167. a) \(\dfrac{1}{3}\) |
168. a) \(-\dfrac{7}{8}\) b) \(-0.03\) c) \(17\) d) \(\dfrac{12}{5}\) |
In the following exercises, find the multiplicative inverse of each number.
| 169. a) 10 b) \(-\dfrac{4}{9}\) c) 0.6 | 170. a) \(-\dfrac{9}{2}\) b) \(-7\) c) 2.1 |
Use the Properties of Zero
In the following exercises, simplify.
| 171. \(83\cdot 0\) | 172. \(\dfrac{0}{9}\) |
| 173. \(\dfrac{5}{0}\) | 174. \(0\)\div \(\dfrac{2}{3}\) |
In the following exercises, simplify.
| 175. \(43+39+\left(-43\right)\) | 176. \(\left(n+6.75\right)+0.25\) |
| 177. \(\dfrac{5}{13}\cdot 57 \cdot \dfrac{13}{5}\) | 178. \(\dfrac{1}{6}\cdot17\cdot12\) |
| 179. \(\dfrac{2}{3}\cdot 28 \cdot \dfrac{3}{7}\) | 180. \(9\left(6x-11\right)+15\) |
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the Distributive Property.
| 181. \(7\left(x+9\right)\) | 182. \(9\left(u-4\right)\) |
| 183. \(-3\left(6m-1\right)\) | 184. \(-8\left(-7a-12\right)\) |
| 185. \(\dfrac{1}{3}\left(15n-6\right)\) | 186. \(\left(y+10\right)\cdot p\) |
| 187. \(\left(a-4\right)-\left(6a+9\right)\) | 188. \(4\left(x+3\right)-8\left(x-7\right)\) |
Review Exercise Answers
| 1. \(\dfrac{2}{8},\dfrac{3}{12},\dfrac{4}{16}\) answers may vary | 3. \(\dfrac{10}{12},\dfrac{15}{18},\dfrac{20}{24}\) answers may vary | 5. \(\dfrac{1}{3}\) |
| 7. \(\dfrac{3}{4}\) | 9. \(-\dfrac{7}{8}\) | 11. \(\dfrac{x}{y}\) |
| 13. \(\dfrac{2}{15}\) | 15. \(-\dfrac{2}{9}\) | 17. \(7p\) |
| 19. \(-42\) | 21. 2 | 23. \(-\dfrac{7}{5}\) |
| 25. \(\dfrac{25}{4a}\) | 27. \(\dfrac{2}{9}\) | 29. \(-\dfrac{1}{25}\) |
| 31. \(\dfrac{3}{4}\) | 33. \(-\dfrac{3}{10}\) | 35. \(\dfrac{3r}{5s}\) |
| 37. \(\dfrac{15}{8}\) | 39. \(-6\) | 41. \(\dfrac{4}{3}\) |
| 43. \(-4\) | 45. \(\dfrac{5}{21}\) | 47. \(-2\) |
| 49. \(\dfrac{c}{d+9}\) | 51. \(\dfrac{5}{9}\) | 53. \(\dfrac{y+2}{3}\) |
| 55. \(-\dfrac{1}{2}\) | 57. \(\dfrac{3}{5}\) | 59. \(\dfrac{y-9}{17}\) |
| 61. \(-\dfrac{11}{d}\) | 63. \(\dfrac{8}{15}\) | 65. \(\dfrac{3}{10}\) |
| 67. \(\dfrac{17}{12}\) | 69. \(\dfrac{13}{24}\) | 71. \(\dfrac{19}{80}\) |
| 73. \(\dfrac{11}{6}\) | 75. \(\dfrac{1}{275}\) | 77. 14 |
| 79. a) \(\dfrac{3}{8}\) b) 0 | 81. \(\dfrac{5}{9}\) | 83. \(-6\) |
| 85. 8.03 | 87. 0.001 | 89. seven and eight tenths |
| 91. five thousandths | 93. a) 5.79 b) 5.8 c) 6 | 95. a) 12.48 b) 12.5 c) 12 |
| 97. 27.73 | 99. −5.53 | 101. −13.5 |
| 103. 35.8 | 105. 42.51 | 107. 0.12 |
| 109. 26.7528 | 111. 2.2302 | 113. 0.03 |
| 115. \$0.71 | 117. 150 | 119. \(\dfrac{2}{25}\) |
| 121. \(\dfrac{17}{40}\) | 123. \(\dfrac{7}{4}\) | 125. 0.4 |
| 127. \(-0.375\) | 129. \(0.\stackrel{\text{–}}{5}\) | 131. 7 |
| 133. a) \(\dfrac{9}{1}\) b) \(\dfrac{847}{100}\) |
135. a) \(0.84,1.\stackrel{\text{–}}{3}\) b) \(0.79132\text{…}\),
|
137. a) 0, 17 b) -4,0,17 c) \(-4,0,\dfrac{5}{6},17\) d) \(5.2537\text{…}\) e) \(-4,0,17,\dfrac{5}{6}, 5.2537\text{…}\) |
139. 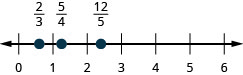 |
141. 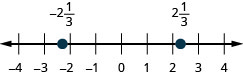 |
143. < |
| 145. > | 147. 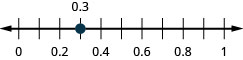 |
149. 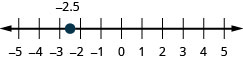 |
| 151. > | 153. > | 155. \(-48m\) |
| 157. \(a+47\) | 159. 37 | 161. \(\dfrac{35}{9}\) |
| 163. \(1\dfrac{7}{12}\) | 165. \(27x+23y\) | 167. a) \(-\dfrac{1}{3}\) b) \(-5.1\) c) 14 d) \(\dfrac{8}{5}\) |
| 169. a) \(\dfrac{1}{10}\) b) \(-\dfrac{9}{4}\)c)\(\dfrac{5}{3}\) | 171. 0 | 173. undefined |
| 175. 39 | 177. 57 | 179. 8 |
| 181. \(7x+63\) | 183. \(-18m+3\) | 185. \(5n-2\) |
| 187. \(-5a-13\) |
Practice Test
| 1. Convert 1.85 to a fraction and simplify. | 2. Locate \(\dfrac{2}{3},-1.5\), and \(\dfrac{9}{4}\) on a number line. |
In the following exercises, simplify each expression.
| 3. \(4+10\left(3+9\right)-{5}^{2}\) | 4. \(-85+42\) |
| 5. \(-19-25\) | 6. \({\left(-2\right)}^{4}\) |
| 7. \(-5\left(-9\right)\)÷\(15\) | 8. \(\dfrac{3}{8}\cdot \dfrac{11}{12}\) |
| 9. \(\dfrac{4}{5}\)÷\(\dfrac{9}{20}\) | 10. \(\dfrac{12+3\cdot 5}{15-6}\) |
| 11. \(\dfrac{m}{7}+\dfrac{10}{7}\) | 12. \(\dfrac{7}{12}-\dfrac{3}{8}\) |
| 13. \(-5.8+\left(-4.7\right)\) | 14. \(100-64.25\) |
| 15. \(\left(0.07\right)\left(31.95\right)\) | 16. 9 ÷ 0.05 |
| 17. \(-14\left(\dfrac{5}{7}p\right)\) | 18. \(\left(u+8\right)-9\) |
| 19. \(6x+\left(-4y\right)+9x+8y\) | 20. \(\dfrac{0}{23}\) |
| 21. \(\dfrac{75}{0}\) | 22. \(-2\left(13q-5\right)\) |
Practice Test Answers
| 1. \(\dfrac{37}{20}\) |  |
3. 99 |
| 4. \(-43\) | 5. \(-44\) | 6. \(16\) |
| 7. \(3\) | 8. \(\dfrac{11}{32}\) | 9. \(\dfrac{16}{9}\) |
| 10 \(3\) | 11. \(\dfrac{m+10}{7}\) | 12. \(\dfrac{5}{24}\) |
| 13. \(-10.5\) | 14. 35.75 | 15. 2.2365 |
| 16. \(180\) | 17. \(-10p\) | 18. \(u -1\) |
| 19. \(15x+4y\) | 20. 0 | 21. undefined |
| 22. \(-26q + 10\) |